07-hashCode与哈希冲突

1. hashCode的特性

（1）HashCode的存在主要是用于查找的快捷性，如Hashtable，HashMap等，HashCode经常用于确定对象的存储地址；

（2）如果两个对象相同， equals方法一定返回true，并且这两个对象的HashCode一定相同；

（3）两个对象的HashCode相同，并不一定表示两个对象就相同，即equals()不一定为true，只能够说明这两个对象在一个散列存储结构中。

（4）如果对象的equals方法被重写，那么对象的HashCode也尽量重写，以保证equals方法相等时两个对象hashcode返回相同的值（eg：Set集合中确保自定义类的成功去重）。

Set集合中元素不重复的基本逻辑判断示意图：

2. hashCode的算法

1. 对象类型的数据，返回的一串字符；
2. String类型的数据，返回一串字符；
3. integer类型的数据，返回的hash值为数据本身；

• Object对hashCode()的方法实现：

public native int hashCode();

该方法返回该对象的十六进制的哈希码值（即，对象在内存中的数字型名字）。

哈希算法根据对象的地址或者字符串或者数字计算出来的int类型的数值。而且哈希码并不唯一，可保证相同对象返回相同的哈希码，只能尽量保证不同对象返回不同的哈希码值。

• String 对hashCode()的方法实现：

public int hashCode() {
    int h = hash;
    if (h == 0 && value.length > 0) {
        char val[] = value;
 
        for (int i = 0; i < value.length; i++) {
            h = 31 * h + val[i];
        }
        hash = h;
    }
    return h;
}

主要探讨一下String对于hashCode算法的实现：

字符串对象的哈希码根据以下公式计算：
s[0]*31^(n-1) + s[1]*31^(n-2) + … + s[n-1]
使用 int 算法，这里 s[i] 是字符串的第 i 个字符，n 是字符串的长度，^ 表示求幂。空字符串的哈希值为 0。

• Integer对hashCode()的实现：

@Override
public int hashCode() {
    return Integer.hashCode(value);
}

3. hashCode的作用

哈希算法：也称为散列算法，是将数据依特定算法直接指定到一个地址上。这样一来，当集合要添加新的元素时，先调用这个元素的HashCode方法，就一下子能定位到它应该放置的物理位置上。

（1）如果这个位置上没有元素，它就可以直接存储在这个位置上，不用再进行任何比较了；

（2）如果这个位置上已经有元素了，就调用它的equals方法与新元素进行比较，相同的话就不存了；

（3）不相同的话，也就是发生了Hash key相同导致冲突的情况，那么就在这个Hash key的地方产生一个链表，将所有产生相同HashCode的对象放到这个单链表上去，串在一起。这样一来实际调用equals方法的次数就大大降低了。

hashCode在上面扮演的角色为寻域（寻找某个对象在集合中区域位置）。

所以，总结一下，hashCode的存在主要是用于查找的快捷性，如Hashtable，HashMap，HashSet等。

hashCode是用来在散列存储结构中确定对象的存储地址的。

4.什么是哈希冲突

哈希冲突（Hash Collision）是指两个或多个不同的数据值被映射到了哈希表中相同的存储地址上。哈希表是一种以键值对形式存储数据的数据结构，其中每个键都会通过哈希函数计算出一个索引值，该索引值作为键在哈希表中的位置，而值则存储在该位置上。但由于哈希函数的输出范围比输入范围小得多，无法避免一定概率的哈希冲突。

• 哈希函数：数据元素的存储地址，是根据数据的关键字K通过一定的函数关系计算得出，这个函数关系即称哈希函数。

• Hash冲突：不同的数据元素关键字K，计算出的哈希值相同，此时两个或多个数据，对应同一个存储地址，即产生冲突。

先通过取模运算来建立一个简单的哈希表：

数据：int[] array = {1，7，6，5，4，8}；

哈希函数：hash(key) = key% 表长; //这里的key为每一个元素的值，表长为10

对于上面的hash表来说，如果现在先插入一个元素为14，这时候通过hash函数计算出来的hash地址为4，很明显地址为4已经有了一个元素4，这时候就会发生哈希冲突。首先由于我们底层的数组一般是小于需要存储关键字的数量，所以引起哈希冲突是不可避免的。

引入哈希表的目的就是为了使查找和处理一个数时（不经过比较）让时间复杂度保持在O(1)，这样就是为了加快查询效率，需要了解如何设计哈希函数以及尽可能地避免哈希冲突的方法。

使用哈希表来存储数据就是将数与存储位置通过一个函数来建立对应关系，之后不经过比较，通过这个函数（哈希函数）的结果就能确定该元素的位置。

5.哈希函数设计原则

• 哈希地址必须在哈希表中
• 哈希函数产生的哈希地址尽可能均匀
• 哈希函数要简单

6.常见的哈希函数

（1）直接定址法

取关键字的某个线性函数为散列地址如：

Hash(key) = A*key+B;

应用场景：查找比较小且连续的情况

（2）除留余数法

哈希函数为：

Hash(key) = key%p //这里的p<=哈希表的长度

（3）平方取中法

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址。

应用场景：不知道关键字的分布且位数又不是很大。

（4）折叠法

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。

使用场景：事先不知道关键字分布，而且关键字位数比较多的情况。

（5）随机数法

选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random为随机数函数。

使用场景：关键字长度不等时使用。

7.解决哈希冲突

散列表的负载调节因子：负载调节因子a=填入表中元素个数/散列表的长度。

由负载调节因子公式可以看出，a越大，散列表中元素越多，散列表空间越来越小，之后放进来的元素就越容易产生哈希冲突。当冲突率太大的话，可以通过降低负载调节因子来降低哈希冲突。要是哈希表中关键字的个数不能改变时，我们就需要扩大哈希表的大小来降低哈希冲突的概率。

发生哈希冲突时，有以下几种常见的解决方法：

1. 开放寻址法：在哈希表中找到下一个可用的空位存储冲突的键值对。

2. 链式法：将哈希表中的每个位置变成一个链表，所有哈希值相同的键值对都存储在这个链表中。

3. 再哈希法：使用另一个哈希函数重新计算键的哈希值，直到没有冲突为止。

4. 建立公共溢出区：将所有哈希冲突的元素都存储在一个特殊的区域，称为溢出桶中。

7.1 解决哈希冲突的第一种方法（闭散列）

什么是闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。

这里将寻找key的下一个位置又有两种方式，分别如下:

（1）线性探测法

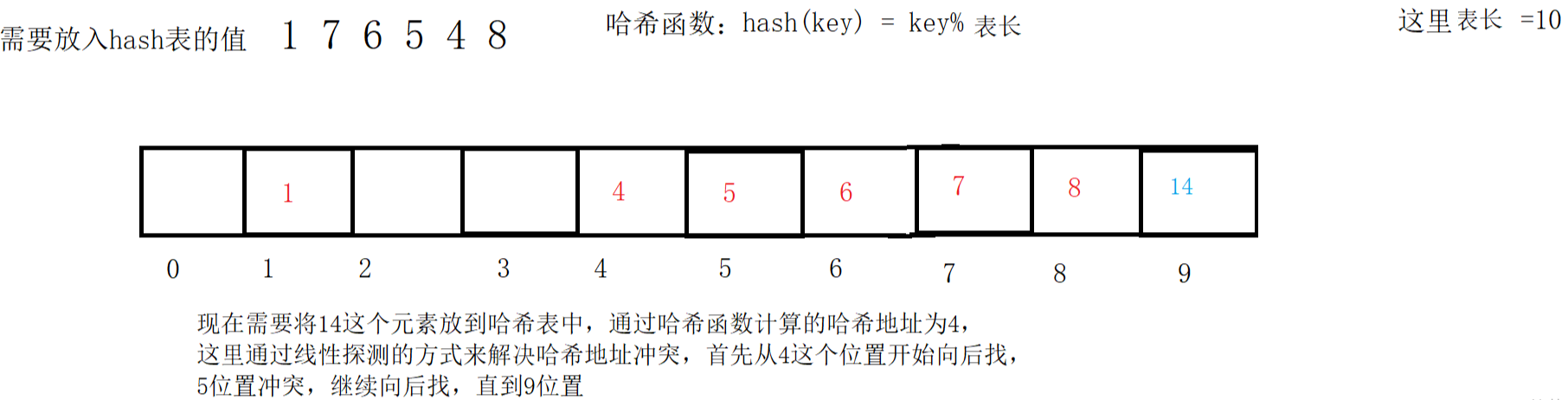
线性探测的缺点：可以看出产生冲突的数据都堆积在一起，而且还不能随意的删除哈希表中已存在的元素，因为直接删除可能会导致其他元素的查找，如果4位置的元素删除后，会影响14元素的查找，这时候我们还需要使用标记的伪元素删除法来删除一个元素（差不多就是标记一下这个元素，之后如果由其他元素可以直接覆盖，但是需要保存这个位置的信息，因为后面的元素可能选哟这个哈希地址再进行线性探测进行寻找）。

（2）二次探测法

寻找空位置的方法：Hi = (H0+i^2)%m

这里的H0就是通过哈希函数计算出来的哈希地址，m为哈希表的大小，i=1,2,3…，这里的i从小到大取，直到不产生哈希冲突即可，最终Hi为元素的存储位置。

7.2 解决哈希冲突的第二种方法（开散列）

（1）开散列/哈希同的概念

开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

（2）哈希桶图示

注意：如果哈希冲突特别严重时，就说明桶下的哈希冲突元素太多，这时候也可以将问题逐渐缩小，解决的方法如：还有哈希表，或者转化为搜索树（思路）。

虽然哈希表一直在和冲突做斗争，但在实际使用过程中，我们认为哈希表的冲突率是不高的，冲突个数是可控的，也就是每个桶中的链表的长度是一个常数，所以，通常意义下，我们认为哈希表的插入/删除/查找时间复杂度是O(1)。